De nombreuses technologies d’aujourd’hui sont basées sur le principe de donner une sortie à une entrée. Mais saviez-vous que ce principe est basé sur les machines à états finis ?
L’attrait de l’IA fascine souvent notre imagination, peignant des images vives de machines intelligentes capables de cognition et de prise de décision de type humain. Pourtant, avant de plonger dans les complexités des systèmes d’IA avancés, nous devons rendre hommage aux ancêtres de l’IA, et aucun n’est plus important que la machine à états finis. Cette construction mathématique élégamment simple sert de pierre angulaire, influençant l’essence même des technologies d’IA telles que nous les connaissons aujourd’hui.
À la base, la machine à états finis est un modèle captivant qui repose sur les principes des états et des transitions discrets. Son architecture comprend un ensemble fini d’états, un tableau de symboles d’entrée, un ensemble optionnel de symboles de sortie et un ensemble de règles qui régissent les transitions entre les états, le tout orchestré avec une simplicité magistrale qui dément sa puissance.

Qu’est-ce qu’une machine à états finis ?
Une machine à états finis (FSM) est un concept fondamental dans le monde de l’informatique et de l’ingénierie. Il sert de modèle mathématique qui nous permet de représenter et de contrôler des systèmes avec des états et des transitions discrets. Cette puissante abstraction est largement utilisée dans divers domaines, de la conception matérielle et du développement logiciel à la robotique et à l’intelligence artificielle.
À la base, un FSM est composé de plusieurs composants clés qui définissent son comportement et sa fonctionnalité. Ces composants comprennent :
États: Le FSM fonctionne dans un ensemble fini d’états, chacun représentant une condition ou une situation spécifique dans le système modélisé. Ces états agissent comme des instantanés de l’état du système à différents moments, reflétant sa configuration interne ou son comportement.
Symboles d’entrée: Le FSM interagit avec l’environnement externe à travers un ensemble de symboles d’entrée. Ces symboles peuvent être n’importe quelle forme de données d’entrée, telles que des caractères, des nombres ou même des données sensorielles provenant de capteurs dans un système robotique.
Symboles de sortie: Dans certains cas, un FSM peut également avoir un ensemble de symboles de sortie associés à des transitions entre états. Ces symboles de sortie représentent la réponse de la machine à des entrées spécifiques et peuvent être utilisés pour communiquer des informations ou déclencher des actions dans le système.
Comment l’intelligence artificielle est passée de la fiction à la science ?
Règles de transition: Le cœur du FSM réside dans l’ensemble de règles qui dictent comment il passe d’un état à un autre en fonction des symboles d’entrée qu’il reçoit. Ces règles, souvent représentées sous la forme d’une table de transition ou d’un diagramme d’état, définissent le comportement et la logique du système modélisé.
Le fonctionnement d’un FSM peut être visualisé comme un flux dynamique entre des états pilotés par les symboles d’entrée qu’il traite. Lorsque la machine démarre, elle entre dans un état initial, qui sert de point de départ à son calcul. Lorsqu’il lit chaque symbole d’entrée, il applique les règles prédéfinies pour déterminer l’état suivant. Ce processus se poursuit jusqu’à ce que la machine à états finis atteigne un état final, signifiant l’achèvement d’une tâche spécifique, ou qu’elle s’arrête en raison d’une transition indéfinie.
Les machines à états finis ont des applications dans divers domaines en raison de leur simplicité, de leur efficacité et de leur polyvalence. Dans la conception matérielle, les FSM sont utilisés pour contrôler les circuits numériques, permettant à des dispositifs tels que des microcontrôleurs, des processeurs et des unités de mémoire d’effectuer des tâches spécifiques en fonction des signaux d’entrée. Dans le développement de logiciels, les FSM jouent un rôle crucial dans des tâches telles que l’analyse lexicale, l’analyse syntaxique et la correspondance d’expressions régulières.

Qui est le fondateur des machines à états finis ?
Le fondateur de la machine à états finis est Edward Forest Moore. Il était un professeur américain de mathématiques et d’informatique, et il a inventé la machine à états finis de Moore en 1956. Le travail de Moore était basé sur les travaux antérieurs de Warren McCulloch et Walter Pitts, qui avaient proposé un modèle mathématique du cerveau humain en 1943.
La machine à états finis de Moore est un type d’automate fini qui a une seule valeur de sortie pour chaque état. Cela contraste avec la machine à états finis de Mealy, qui a une valeur de sortie distincte pour chaque paire d’états d’entrée. Les machines à états finis de Moore sont plus simples à mettre en œuvre que les machines de Mealy, et elles sont souvent utilisées dans les circuits numériques et les logiciels.
Quels sont les différents types de machines à états finis ?
Les machines à états finis (FSM) sont de différents types, chacune offrant des caractéristiques et des fonctionnalités uniques qui répondent à des applications spécifiques. Comprendre ces différents types est crucial pour concevoir des systèmes efficients et efficaces.
Machines à états finis déterministes (DFSM)
Les machines à états finis déterministes sont le type de FSM le plus simple et le plus courant. Dans un DFSM, pour chaque état et symbole d’entrée, il existe précisément une transition définie vers l’état suivant. Ce comportement déterministe signifie qu’étant donné un symbole d’entrée spécifique et l’état actuel, la machine passera toujours au même état suivant. La transition est sans ambiguïté, conduisant à un résultat prévisible.
Les DFSM sont particulièrement utiles dans les applications où le comportement doit être bien défini et où la certitude du fonctionnement de la machine est essentielle. Ils excellent dans les scénarios qui nécessitent un contrôle précis et où il n’y a pas besoin de branchement ou de plusieurs résultats possibles basés sur le même symbole d’entrée.
Machines à états finis non déterministes (NFSM)
Les machines à états finis non déterministes, contrairement aux DFSM, permettent de multiples transitions à partir d’un état pour un symbole d’entrée donné. Ce non-déterminisme introduit une ramification et une ambiguïté dans le comportement de la machine, car il peut y avoir différents chemins possibles que la machine peut suivre en fonction du même symbole d’entrée et de l’état actuel.
Les NFSM sont avantageux dans les situations où plusieurs choix ou décisions valides peuvent être faits sur la base de la même entrée. Ils offrent une représentation plus flexible et expressive, permettant au FSM d’explorer simultanément diverses possibilités. Cette caractéristique est particulièrement utile dans les applications complexes qui impliquent des algorithmes de prise de décision, de résolution de problèmes et de recherche.

Machines farineuses et machines Moore
Outre la distinction entre les FSM déterministes et non déterministes, il existe deux catégories supplémentaires basées sur la manière dont la sortie est déterminée pendant les transitions :
- Machines farineuses
- Machines Moore
Machines farineuses
Dans Mealy Machines, la sortie est déterminée à la fois par l’état actuel et le symbole d’entrée pendant les transitions. Cela signifie que la sortie est associée aux transitions entre les états plutôt que d’être liée uniquement à l’état actuel. En conséquence, les machines Mealy ont tendance à avoir des représentations plus compactes car elles n’ont pas besoin d’associer la sortie à chaque état.
Les machines Mealy sont souvent utilisées dans des applications où la sortie est directement liée à l’entrée et le comportement de la machine nécessite une réactivité aux modifications des symboles d’entrée. Ils sont bien adaptés aux tâches qui impliquent le traitement des données, le traitement du signal et les systèmes en temps réel.
Machines Moore
D’autre part, les machines Moore génèrent une sortie basée uniquement sur l’état actuel et ne prennent pas en compte le symbole d’entrée lors des transitions. Cela signifie que la sortie reste constante pendant la durée où le FSM est dans un état particulier et ne change que lorsque la machine passe à un état différent.
Les machines Moore sont couramment utilisées dans des applications où la sortie dépend uniquement de l’état interne actuel du système. Ils sont bien adaptés aux tâches où la sortie est pilotée par les caractéristiques de l’état et ne nécessite pas de réactivité immédiate aux changements des symboles d’entrée.
Comment fonctionnent les machines à états finis ?
Les machines à états finis (FSM) fonctionnent sur un principe simple et élégant, qui consiste à effectuer une transition entre différents états en fonction des symboles d’entrée qu’ils reçoivent.
Décomposons le processus étape par étape.
États et transitions
Au cœur d’une machine à états finis se trouvent les états. Un état représente une condition ou une situation spécifique dans laquelle la machine peut se trouver à un moment donné. Par exemple, imaginez un feu tricolore avec trois états : « Rouge », « Jaune » et « Vert ». Chacun de ces états représente une condition différente du feu de signalisation.
Le FSM a également des transitions, qui définissent comment il passe d’un état à un autre en fonction de l’entrée qu’il reçoit. Les transitions sont généralement déclenchées par des symboles d’entrée. Ces symboles peuvent être des lettres, des chiffres ou tout autre symbole pertinent pour l’application du FSM.
Etat initial
Lorsqu’une machine à états finis commence son fonctionnement, elle commence dans un état initial. L’état initial est le point de départ du calcul de la machine. Il sert de point d’entrée au FSM pour commencer à traiter l’entrée.
Lecture des symboles d’entrée
Une fois que la machine à états finis est dans l’état initial, elle commence à lire les symboles d’entrée un par un. La machine lit un symbole d’entrée à partir du flux d’entrée, le traite, puis procède à la lecture du symbole d’entrée suivant.
Règles de transition
Pour chaque combinaison d’état et de symbole d’entrée, il existe des règles de transition prédéfinies qui dictent comment le FSM doit répondre. Ces règles déterminent l’état suivant vers lequel la machine doit passer lorsqu’elle rencontre un symbole d’entrée spécifique dans un état donné.
Pour illustrer cela, considérons un FSM simple avec trois états : « A », « B » et « C » et deux symboles d’entrée : « 0 » et « 1 ». Les règles de transition pour ce FSM pourraient être :
- Si le FSM est dans l’état « A » et reçoit le symbole d’entrée « 0 », il passe à l’état « B »
- Si le FSM est dans l’état « A » et reçoit le symbole d’entrée « 1 », il reste dans l’état « A »
- Si le FSM est dans l’état « B » et reçoit le symbole d’entrée « 0 », il passe à l’état « C »
- Si le FSM est dans l’état « B » et reçoit le symbole d’entrée « 1 », il reste dans l’état « B »
- Si le FSM est dans l’état « C » et reçoit le symbole d’entrée « 0 », il revient à l’état « A »
- Si le FSM est dans l’état « C » et reçoit le symbole d’entrée « 1 », il passe à l’état « B »
Transition entre les états
Lorsque le FSM lit chaque symbole d’entrée, il applique les règles de transition pour déterminer l’état suivant. Il suit les transitions définies jusqu’à ce qu’il atteigne un état final ou s’arrête.
États finaux et arrêt
Une machine à états finis peut avoir un ou plusieurs états finaux. Lorsque le FSM atteint un état final après avoir traité les symboles d’entrée, cela signifie qu’il a terminé sa tâche ou atteint un objectif spécifique. La machine peut alors produire une sortie ou déclencher une action associée à cet état final.
En variante, le FSM peut s’arrêter sans atteindre un état final s’il rencontre un symbole d’entrée pour lequel aucune règle de transition valide n’est définie. Dans ce cas, le FSM peut arrêter son fonctionnement sans terminer la tâche pour laquelle il a été conçu.
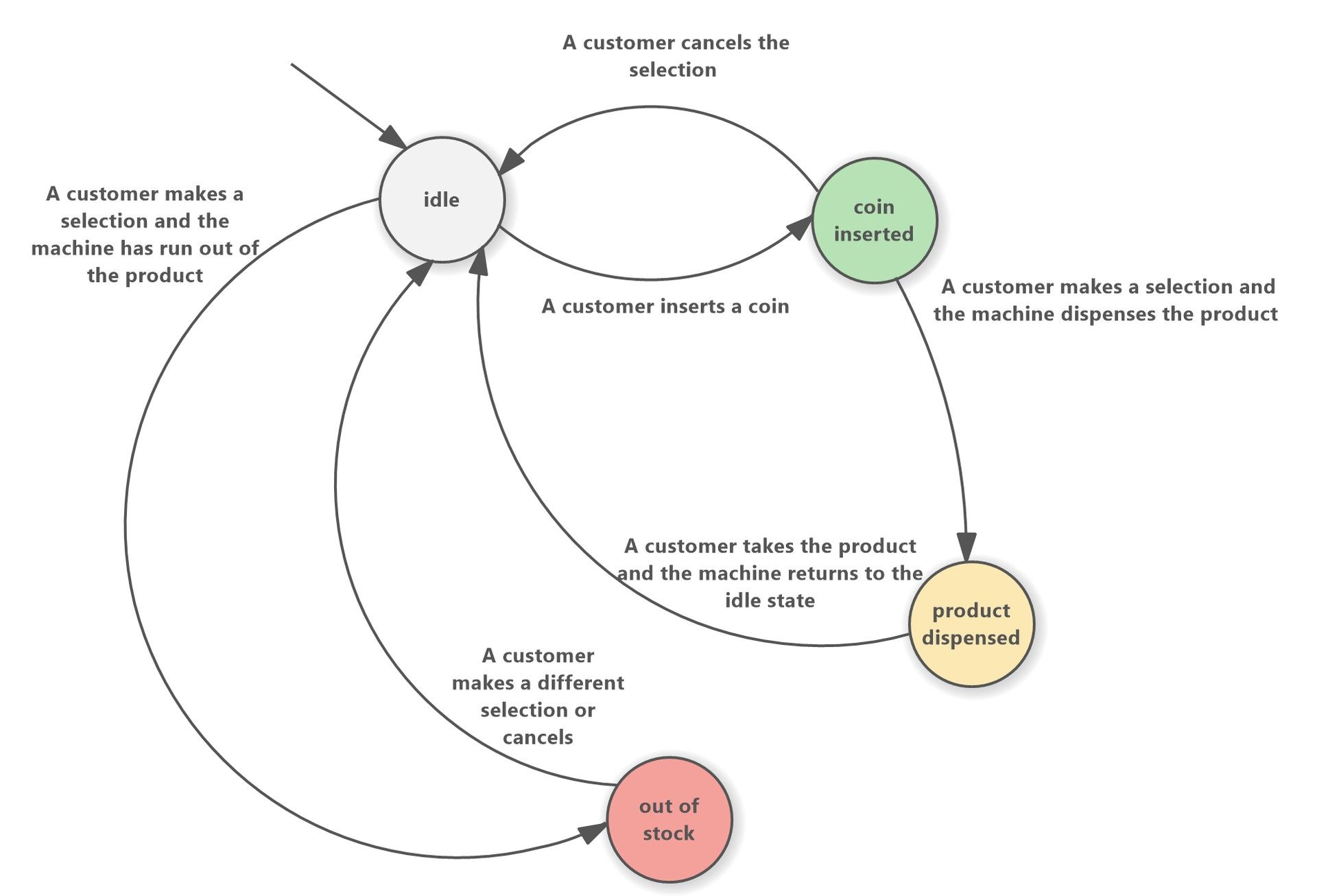
Les machines à états finis sont bien plus que de simples distributeurs automatiques
Les machines à états finis (FSM) se sont révélées être des outils polyvalents avec des applications dans divers domaines. Leur simplicité, leur efficacité et leur capacité à modéliser des comportements séquentiels les rendent précieux dans divers domaines.
Contrôle des machines et appareils
Les machines à états finis jouent un rôle essentiel dans le contrôle de diverses machines et appareils en spécifiant leur comportement en fonction des entrées. Dans ce contexte, les FSM agissent comme des unités de prise de décision qui régissent les actions des machines. Par exemple, dans l’automatisation industrielle, les FSM peuvent être utilisés pour contrôler des processus complexes dans des usines de fabrication.
Le FSM définit les différents états dans lesquels la machine peut se trouver, tels que « Idle », « Processing » et « Shutdown ». Sur la base des entrées des capteurs et d’autres facteurs externes, le FSM passe d’un état à l’autre, contrôlant les opérations de la machine et assurant un fonctionnement efficace.
Programmation informatique
Dans le développement de logiciels, les FSM sont largement utilisés pour diverses tâches. Une application courante est l’analyse lexicale, où les machines à états finis aident à segmenter le code source en composants significatifs tels que des mots-clés, des identifiants et des opérateurs.
Le FSM traite le flux d’entrée caractère par caractère, passant d’un état à l’autre pour identifier et extraire les jetons appropriés. De plus, les FSM sont utilisés pour l’analyse, où ils analysent la syntaxe d’un programme basé sur une grammaire, et pour la correspondance d’expressions régulières, où ils correspondent efficacement aux modèles dans les chaînes.
Systèmes automatisés
Les FSM font partie intégrante des systèmes d’automatisation, permettant un contrôle efficace et fiable des processus. Dans la fabrication, les FSM sont utilisés pour gérer les chaînes de montage, surveiller la qualité des produits et optimiser les flux de production.
Les processus d’automatisation s’appuient sur les FSM pour prendre des décisions, déclencher des actions et garantir que les tâches sont effectuées systématiquement et sans erreur.

Protocoles de communication
Les protocoles de communication utilisent souvent des FSM pour gérer la transmission de données et la gestion des erreurs. Par exemple, dans les protocoles de réseau comme TCP/IP, les FSM gèrent l’établissement et la terminaison des connexions entre les appareils.
Les FSM garantissent que les paquets de données sont transmis correctement, et si des erreurs se produisent pendant la transmission, le FSM gère la retransmission des données perdues pour maintenir l’intégrité et la fiabilité des données dans le processus de communication.
Robotique
Les FSM sont essentiels pour définir le comportement et les processus décisionnels des robots dans divers scénarios. Les robots fonctionnent dans des environnements dynamiques et imprévisibles, et les machines à états finis fournissent une approche structurée pour modéliser leurs réponses aux entrées sensorielles et aux stimuli externes.
Par exemple, dans un robot mobile naviguant dans un labyrinthe, un FSM peut guider ses mouvements en fonction des entrées de capteurs, lui permettant de prendre des décisions sur son chemin, d’éviter les obstacles et d’atteindre sa destination efficacement.
Intelligence artificielle
Les machines à états finis sont les prédécesseurs des technologies d’IA plus complexes, jetant les bases d’une prise de décision séquentielle dans les systèmes d’IA. Alors que les machines à états finis elles-mêmes ont des limites dans la gestion de tâches très complexes et dynamiques, elles ont influencé le développement de modèles et d’algorithmes d’IA plus avancés.
La prise de décision séquentielle, un aspect clé des systèmes d’IA, s’inspire des principes des FSM, où une série de décisions conduisent à un résultat spécifique basé sur des signaux d’entrée.
Développement de jeux
Les machines à états finis sont utilisées pour contrôler le comportement des personnages, gérer les états du jeu et gérer la logique du jeu. Les jeux impliquent souvent des personnages avec des comportements et des interactions spécifiques. Les FSM fournissent un moyen structuré de définir ces comportements et permettent aux personnages de répondre aux entrées des joueurs et aux événements de jeu de manière appropriée.
Les FSM peuvent représenter les différents états d’un personnage, tels que « Idle », « Courir », « Sauter » et « Attaquer », et la transition entre ces états en fonction des actions du joueur et des événements de jeu, créant des expériences de jeu engageantes et dynamiques.
On ne peut s’empêcher de se demander si Edward Forrest Moore a jamais imaginé que cet algorithme simple mais inspirant qu’il a créé offrirait cette technologie à l’humanité en 2023.
Pendant que nous attendons avec curiosité de voir ce que l’IA et la robotique peuvent encore accomplir, nous lui rendons hommage.
Crédit image en vedette : Photo par Chris Briggs sur Unsplash.